Parabolic Equations
Parabolas are conic sections, which can open up, down, left or right. Let's consider these in turn:
Consider this conic form for a parabola equation:
(x-h)2 = 4p(y-k)
It tells you several things:
- It opens either up or down since it begins with (x-h)2.
- If 4p is positive, it opens up. If 4p is negative, it opens down.
- The vertex is (h, k) and that is the point at the at the bottom of the "U" for an upward-opening parabola or the top of the "∩" for a downward-opening parabola.
- The focus is the point around which the parabola opens. It is within the "U" for instance and is a distance p away from the vertex. So, an upward-opening parabola will have a focus of (h, k+p). A dowward-opening parabola will have a focus of (h, k-p).
- The directrix is the line a distance p from the vertex, and the parabola opens away from the directrix. So, the directrix for an upward-opening parabola is y = k-p. And the directrix for a downward-opening parabola is y = k+p.
Summary
(x-h)2 = 4p(y-k)
| 4p | Opening | Vertex | Focus | Directrix |
|---|
| Positive | Upward | (h,k) | (h,k+p) | y = k-p |
| Negative | Downward | (h,k) | (h,k-p) | y = k+p |
An upward-opening parabola:

Example: (x-7)2 = 24(y-3)
- Starts with (x-7)2, and 4p is 24, which is positive. That which means it opens upward. It also means p is 6 (by simply doing |24/4|. Why absolute value? Because a measure in distance is always non-negative).
- Vertex: (7,3)
- Focus: (7,9)
- Directrix: y = -3 (which is calcuated from k-p = 3-6 = -3)
Example: (x+5)2 = -32(y+11)
- Starts with (x+5)2, and 4p is -32, which is negative. That which means it opens downward. It also means p is 8 (by simply doing |32/4|).
- Vertex: (-5,-11) What's with the negative numbers? Well (x+5) is (x-(-5)) and (y+11) is (y-(-11)).
- Focus: (-5,-19)
- Directrix: y = -3
Consider this conic form for a parabola equation:
(y-k)2 = 4p(x-h)
It tells you several things:
- It opens either right or left since it begins with (y-k)2.
- If 4p is positive, it opens right. If 4p is negative, it opens left.
- The vertex is (h, k) and that is the point at the at the "left mid-point" on the "⊂" for a right-opening parabola or the "right mid-point" on the "⊃" for a left-opening parabola.
- The focus is the point around which the parabola opens. It is within the "⊂" for instance and is a distance p away from the vertex. So, a right-opening parabola will have a focus of (h+p, k). A left-opening parabola will have a focus of (h-p, k).
- The directrix is the line a distance p from the vertex, and the parabola opens away from the directrix. So, the directrix for a right-opening parabola is x = h-p. And the directrix for a left-opening parabola is x = h+p.
Summary
(y-k)2 = 4p(x-h)
| 4p | Opening | Vertex | Focus | Directrix |
|---|
| Positive | Right | (h,k) | (h+p,k) | x = h-p |
| Negative | Left | (h,k) | (h-p,k) | x = h+p |
A right-opening parabola:
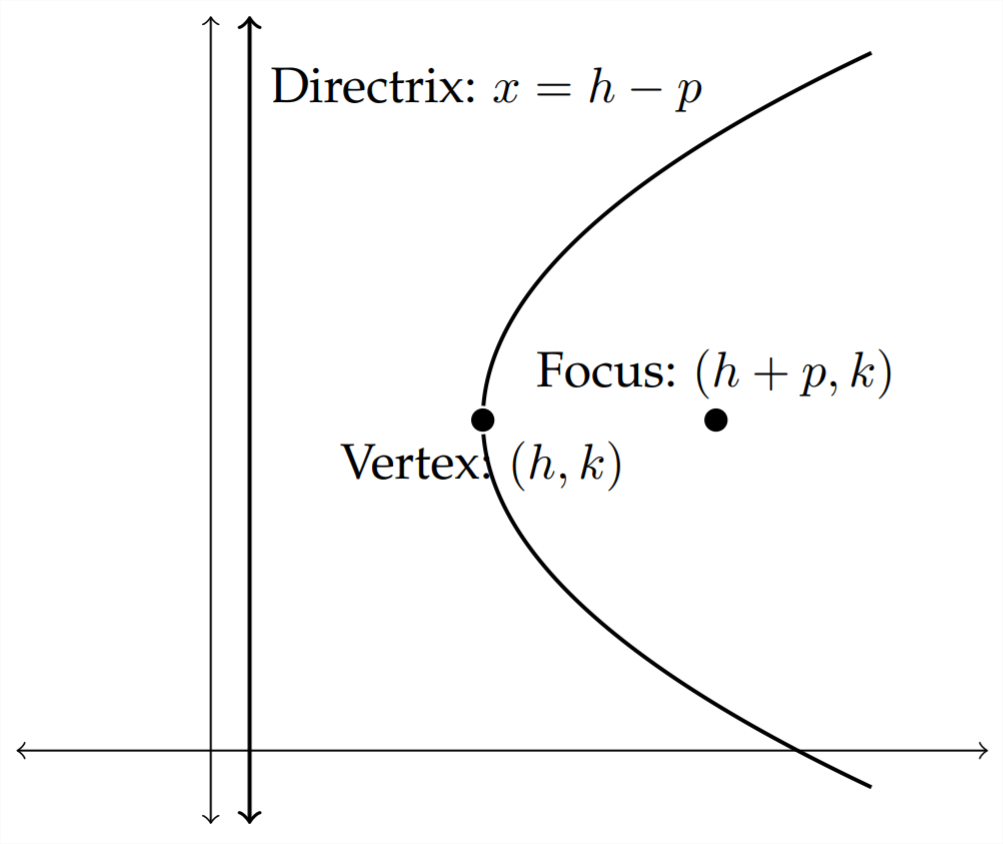
Example: (y-7)2 = 24(x-3)
- Starts with (y-7)2, and 4p is 24, which is positive. That which means it opens right. It also means p is 6.
- Vertex: (3,7)
- Focus: (9,7)
- Directrix: x = -3
Example: (y+5)2 = -32(x+11)
- Starts with (y+5)2, and 4p is -32, which is negative. That which means it opens left. It also means p is 8.
- Vertex: (-11,-5)
- Focus: (-19,-5)
- Directrix: x = -3
Math Help
